Et si on apprenait à compter en binaire, avec des 1 et des 0 ?

 Rappel mathématique :

Activité "Écriture binaire des nombres"

 Fiche d’activité :

 Jeu de cinq cartes binaires :

Il existe des activités supplémentaires en option, pour lesquelles les enfants ont besoin des éléments suivants : (télécharger le document complet)

• L’exercice : Travailler en binaire (page 7)
• L’exercice : Envoyer des messages secrets (page 8)
• L’exercice : Télécopieurs et modems (page 9)
• L’exercice : Compter au-delà de 31 (page 10)
• L’exercice : En savoir plus sur l’écriture binaire des nombres (page 11)

Activité "Tour de magie"

Cette activité est présentée de manière détaillée sur le site https://culturemath.ens.fr.

 Déroulement du tour

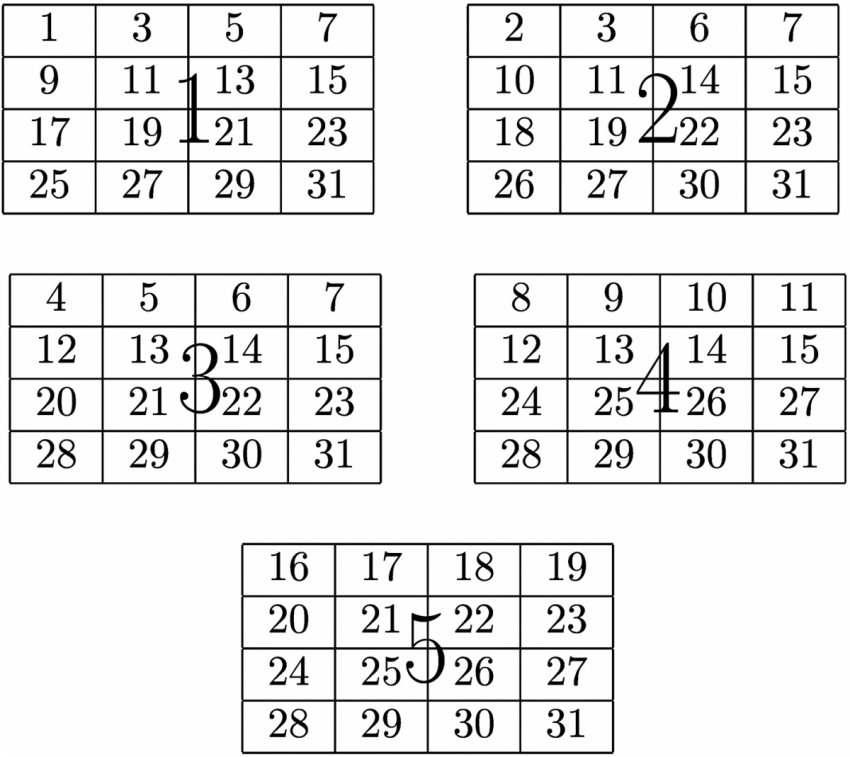
Le magicien (l’enseignant) demande à un spectateur (un élève) de choisir secrètement un nombre entre 0 et 31. En posant cinq questions, le magicien découvre le nombre secret. Pour cela, il dispose des cinq cartes de la figure 1. Ces cartes comportent chacune seize cases contenant les nombres indiqués.

Le magicien montre les cartes une par une (dans l’ordre) au spectateur. Chaque fois, il demande si le nombre secret est présent ou non sur la carte. Une fois qu’il a obtenu la réponse aux cinq questions, le magicien trouve le nombre choisi par le spectateur !

 Fonctionnement du tour

Le magicien mémorise les cartes pour lesquelles le spectateur a répondu que le nombre secret est présent. Si par exemple, il s’agit des cartes n°1, 3 et 4, alors ce nombre est 13 = 1 + 4 + 8. Les termes de la somme sont les premiers nombres (en haut à gauche) de chaque carte pour laquelle le spectateur a indiqué que son nombre secret était présent. Plus précisément, si le spectateur indique la carte i, alors le magicien mémorise 2^(i-1). Une fois toutes les cartes passées, il suffit de sommer les nombres mémorisés. Ainsi, sur l’exemple précédent, le magicien obtient le nombre secret comme suit :

En effet, les nombres présents sur la carte i sont exactement ceux dont l’écriture binaire présente un 1 en position i (en partant de la droite), ce qui correspond à l’utilisation de 2^(i-1) dans la décomposition en somme de puissances de 2. Ainsi, le nombre 13 s’écrit 1101 en binaire. Les cinq cartes permettent de découvrir tous les nombres dont l’écriture binaire utilise au plus cinq chiffres, c’est-à-dire ceux entre 0 et 31.

 En classe

La phase de recherche : les élèves ont l’habitude de ce type d’exercices. Ils émettent spontanément différentes hypothèses, avant de venir les tester devant la classe en tentant de reproduire eux-mêmes le tour. Lors de cette phase, dans une classe, des élèves ont émis l’hypothèse que l’enseignant regardait et mémorisait chacune des cartes retenues puis qu’il était capable de donner le seul nombre apparaissant sur toutes ces cartes. Pour démontrer que cela n’est pas le cas, le tour a été réalisé les yeux bandés (puisque l’ordre des cartes suffit pour retrouver le nombre). Au bout de quelques minutes et de quelques essais, dans toutes les classes, les élèves ont l’idée que l’enseignant effectue un calcul. Certains élèves, ayant une idée précise, remplacent le magicien afin de tester leur hypothèse. En cas d’échec, un autre élève est invité à essayer, en cas de réussite, un autre essai est proposé au même élève. Après plusieurs tentatives, (environ 20 minutes) un élève réussit à tous les coups à retrouver le nombre choisi. Dans ce cas, le professeur demande à l’élève de décrire à ses camarades comment il procède. Ensuite l’enseignant reformule à son tour le fonctionnement du tour.

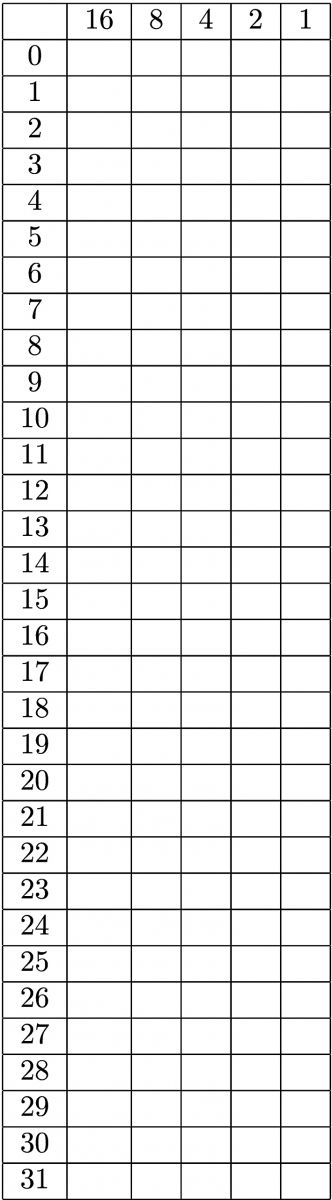
Dans un deuxième temps, l’enseignant propose de montrer comment construire les cartes magiques. Pour cela, les élèves doivent compléter le tableau de la figure 2. La consigne pour remplir le tableau est de décomposer chaque nombre en somme dont les termes sont 1, 2, 4, 8 et 16.

Autrement dit, pour chaque ligne numérotée de 0 à 31, il s’agit de mettre des 1 dans toutes les colonnes dont l’en-tête est utilisé dans la décomposition de ce nombre, et des 0 dans les autres colonnes.

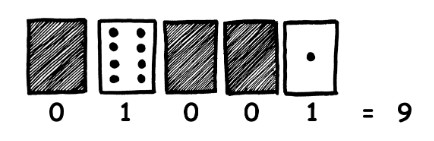
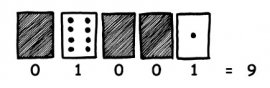
Exemple : On décompose 9 en faisant 8 + 1

L’enseignant donne aux élèves un exemple pour illustrer la consigne. Ce tableau permet de construire la représentation en binaire de tous les nombres entre 0 et 31. Ensuite, pour construire la carte numéro 1, il suffit de recopier dans l’ordre croissant les nombres pour lesquels un 1 est présent dans la dernière colonne du tableau. Il reste alors à procéder de même avec les quatre autres colonnes pour construire les quatre autres cartes.

L’enseignant peut faire coller le tableau sur le cahier des élèves avec en titre « Écriture binaire des nombres ». Sous le tableau, les élèves notent que l’écriture des nombres utilisant des 0 et des 1 s’appelle l’écriture en base 2. En remarque, ils notent que l’écriture habituelle est l’écriture en base 10. Puis des exemples sont proposés pour illustrer ces deux notions.

Pendant la recherche ou pendant l’explication, dans toutes les classes, des élèves remarquent que les premiers nombres (en haut à gauche) de chaque carte, qui servent à écrire les décompositions, doublent d’une carte à l’autre. Ainsi il est naturel de demander par quel nombre débuterait la carte suivante : ici la carte numéro 6, qui débuterait donc par 2⁵ = 32. Il est alors possible de demander aux élèves de construire à la maison les cartes pour pouvoir deviner des nombres entre 0 et 63. Pour préparer ce travail, l’enseignant peut demander :

 Quel est le premier nombre de la carte numéro 6 ?

 Avec 6 cartes, le tour permettrait de deviner des nombres allant de quel nombre jusqu’à quel nombre ?

 Les nouvelles cartes auront-elles le même nombre de cases que celles utilisées en classe ?

 Combien de cases les nouvelles cartes auront-elles ?

 Comment construire les nouvelles cartes ?